음수 표현

컴퓨터는 N개의 비트를 이용하여 2^N개의 정수를 표현할 수 있다. 이러한 방식으로 인하여 수 표현이 쉽지 않다.(또한 정수와 음수를 표현하기 위해 +, -도 표현해야 됨)

보수란, 어떤 수를 보충해주는 수를 말한다. 예를 들어 10진수 4에 대한 10의 보수는 6, 12에 대한 10의 보수는 88이다. 즉, n의 보수는 어떤 수에 대해 n의 제곱수가 되도록 만드는 수

보수는 컴퓨터에서 음의 정수를 표현하기 위해 고안되었다. 컴퓨터 내부에서 사칙연산할 때 던셈을 담당하는 가산기(adder)만 이용하기 때문에 뺄셈은 덤셈으로 형식을 변환하여 계산한다. 즉, A - B를 계산할 때 B의 보수(-B)를 구한 다음 A + (-B)로 계산하게 된다,.

1. 7 - 2 = 5
2. 10진수 2의 보수는 -2
3. 7 + (-2) = 5

10진법이면, n의 보수는 어떤 수에 대해 n의 제곱수가 되도록 만드는 수

• 4에 대한 2의 보수
• 4 + ? = 2^2
• 4 + ? = 4
• 4 + 0 = 4
• 4에 대해 2의 제곱근(4)이 되도록 만드는 수는 0이다.

2진법에서 1의 보수

모든 자리 수를 1로 만드는 수를 구하면 된다.

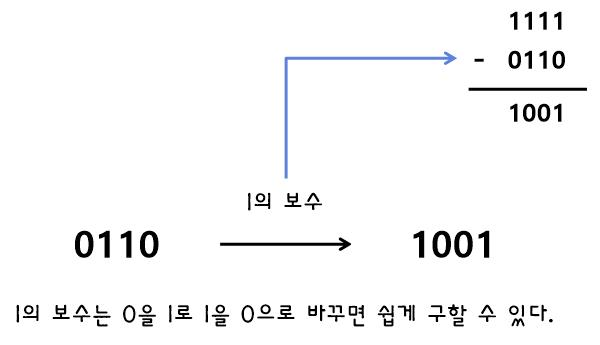
모든 수의 1의 보수는 비트가 반전되기 때문에 구하기 쉽다.

2진법에서 2의 보수

1의 보수를 구한 뒤 1을 더하면 2의 보수가 나온다.

대부분 컴퓨터에서 음수를 표현할 때 2의 보수를 활용한다.

이유는

• 덧셈만으로 뺄샘구현 가능
• 1의 보수의 단점(캐리 발생, 두 부호를 가지는 0) 해결