자료구조와 알고리즘에 대해서

March 13th, 2022

Data structure & Algorithm

왜 배워야 되는가?

문제 해결에 있어서 빠르고 효율적이게 해결하기 위함

자료구조

데이터는 오일과 같다. 정부, 기업 등은 사용자의 데이터를 원하는데, 때문에 서비스가 무료이고 데이터를 통해 AI를 훈련시킬 수 있기 때문이다.

어떠한 상황에서도 데이터를 다룬다. FE는 서버에서 받은 json 데이터를 UI/UX에 맞게 표현해야하고, BE는 DB를 통해 데이터를 insert, select, update, delete 한다. 결국 자료구조(Data structure)는 이 데이터를 정리하는 것으로 데이터를 어떻게 정리하느냐에 따라서 스피드에 영향을 준다.

어떤 자료구조를 사용함에 따라 서비스가 빠르거나 혹은 느려진다. 그리고 그 자료구조는 여러개가 될 수 있는데 어떤 자료구조는 검색에 최적화되고 정렬에 최적화되는 등 여러가지이다.

따라서 어떠한 작업에 적합한 자료구조를 언제 어떻게 사용하는 것이 중요하다.

알고리즘

여러개의 지시사항, 어떠한 액션을 처리하기 위해 컴퓨터가 수행해야하는 것들이다. (훌륭한 알고리즘은 재활용이 가능하다.)

예를 들어, 커피를 마시기위해 하는 일련의 행동들 즉, 목적을 달성하기 위한 여러개의 행동들을 통해 결과를 산출한다. 컴퓨터에서는 지도의 Path finder, 무손실 압축, 암호화 알고리즘 등이 있다.

시간복잡도(Time Complexity)

프로그램을 작성하는데 입력에 따라 연산하는 횟수가 달라진다. 입력된 자료의 양과 알고리즘 실행에 걸리는 사이에는 어느 정도의 관계가 있는데, 이것을 알고리즘의 시간복잡도라 한다.

BigO 표기법

알고리즘 속도의 표현법으로 예를 들어, 선형 검색(Linear Search)의 시간복잡도를 표현하면 O(N)이 된다.

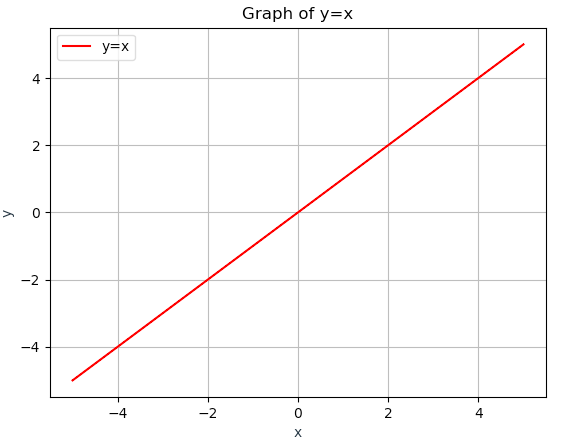
Untitled

이렇게 쓰는 이유는 빠르고 이해하기 쉽기 때문이다.

  • 일반표현 → 배열의 크기가 N개면, N개의 절차가 필요하다.
  • Big O 표기법 → O(N)

아래와 같이 읽기 쉽고, 바로 설명이 가능하다. Big O를 이해하면 알고리즘 분석을 빠르게 할 수 있고, 언제 무엇을 쓸지 빠르게 파악이 가능하다. 또한 자신의 코드가 미래에 어떻게 작동할지 확인이 가능하기 때문에 평가가 가능하다.

절차, 시간복잡도의 기준

시간복잡도의 빠르다 혹은 느리다를 시간으로 표현하지 않는다. 이유는 프로그램의 연산을 처리하는 것은 하드웨어이고, 각각의 사용자가 다른 하드웨어를 사용하기 때문이다. 따라서 알고리즘 스피드는 완료까지 걸리는 절차의 수로 결정된다.

예를 들어, 10개의 절차를 수행하는 알고리즘보다 5개의 절차를 수행하는 알고리즘이 훌륭한 알고리즘이다.

1 2 3 4 5 6 7 8 9 10 배열A(절차 10개 수행)
a b c d e           배열B(절차 5개 수행) Win

상수 시간(Constant Time)

입력받는 자료의 크기와 상관없이 동일한 절차를 수행한다. 이를 시간복잡도로 상수시간(Constant Time)이라고 부르며, Big O 표기로 O(1) 라고 한다.

항상 같은 수의 절차를 수행하기 때문에 가장 선호하는 알고리즘이다.

def printFirst(arr):
	print(arr[0])

Untitled

잘못된 Big O 표기

def printTwice(arr):
	print(arr[0])
	print(arr[1])
# O(2)?

위의 함수를 변형해서 두 번의 절차를 수행하는 함수이다. 똑같은 Constant Time이지만 O(2)로 표기하지 않고 똑같이 O(1)로 표기한다.

Big O는 디테일에 신경쓰지 않고 러프하게 큰 원리를 따른다. 아무리 많은 입력 자료가 들어와도 똑같은 수의 절차를 수행하는 알고리즘은 O(1)으로 표기한다. 즉, 상수(Constant)에 신경쓰지 않는다.

선형 시간(Linear time)

입력 받는 자료의 크기에 따라 선형으로 절차가 증가한다. 이를 선형(Linear time)이라고 부르며, O(N)이라고 표기한다.

def printAll(arr):
	for n in arr:
		print(n)

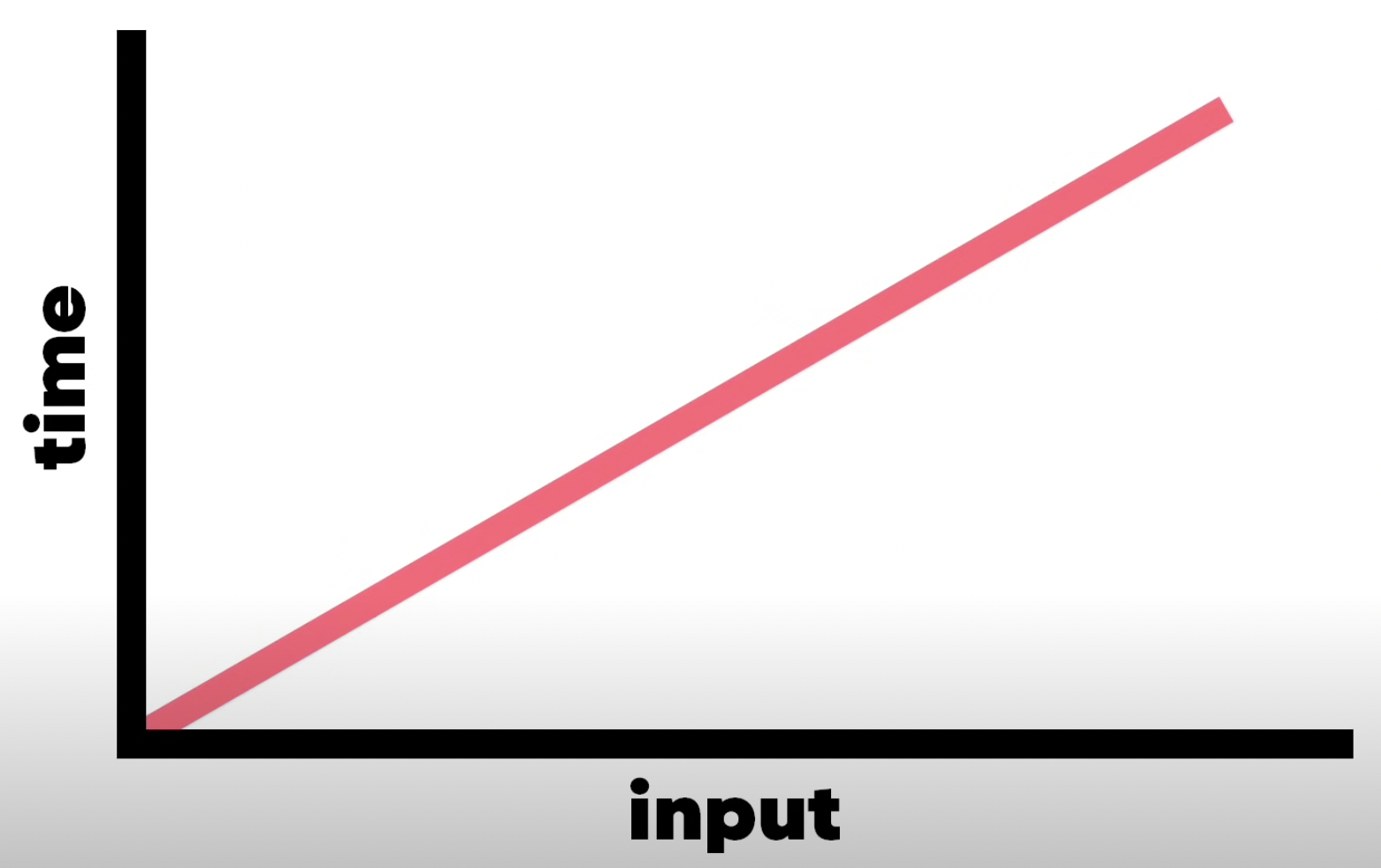
Untitled

선형 시간은 상수와 관계가 없다. 예를 들어 for를 두번 반복하는 함수가 있다.

def printAllTwice(arr):
	for n in arr:
		print(n)
	for n in arr:
		print(n)

하지만 입력 값에 비례해 절차도 증가한다는 본질은 바뀌지 않았기 때문에 O(2N)이라고 하지 않고 O(N)이다.

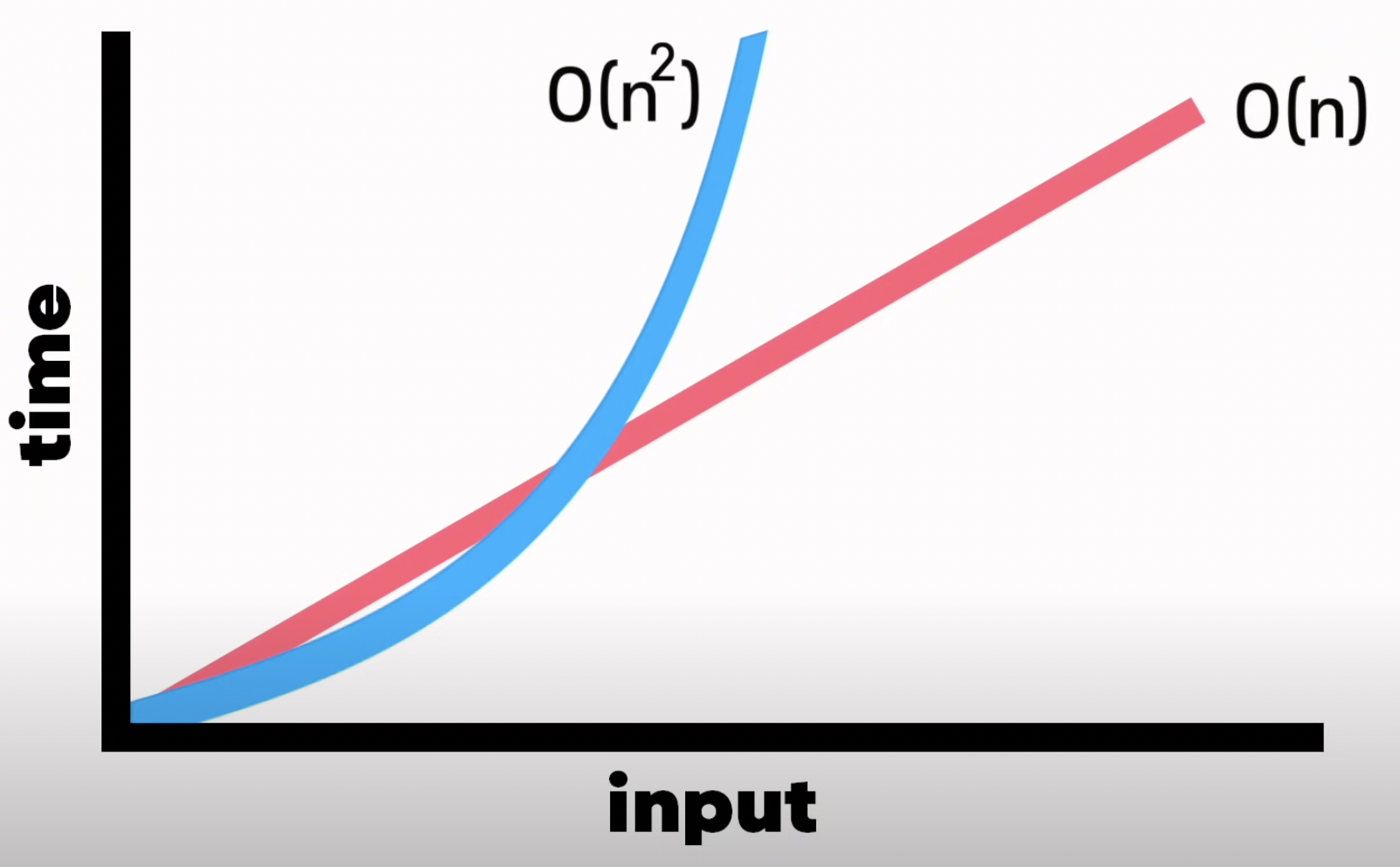
2차 시간(Quadratic Time)

2차 시간은 중첩 반복(Nested Loops)이 있을 때 발생한다. 예를 들면 아래와 같다.

def printTwice(arr):
	for n in arr:
		for x in arr:
			print(x, n)

시간복잡도는 입력 값의 n^2이므로, O(N^2)로 표기한다.

루프안에 루프가 실행되기 때문에 2차 시간(Quadratic Time)보다는 선형 시간(Linear Time)이 선호된다.

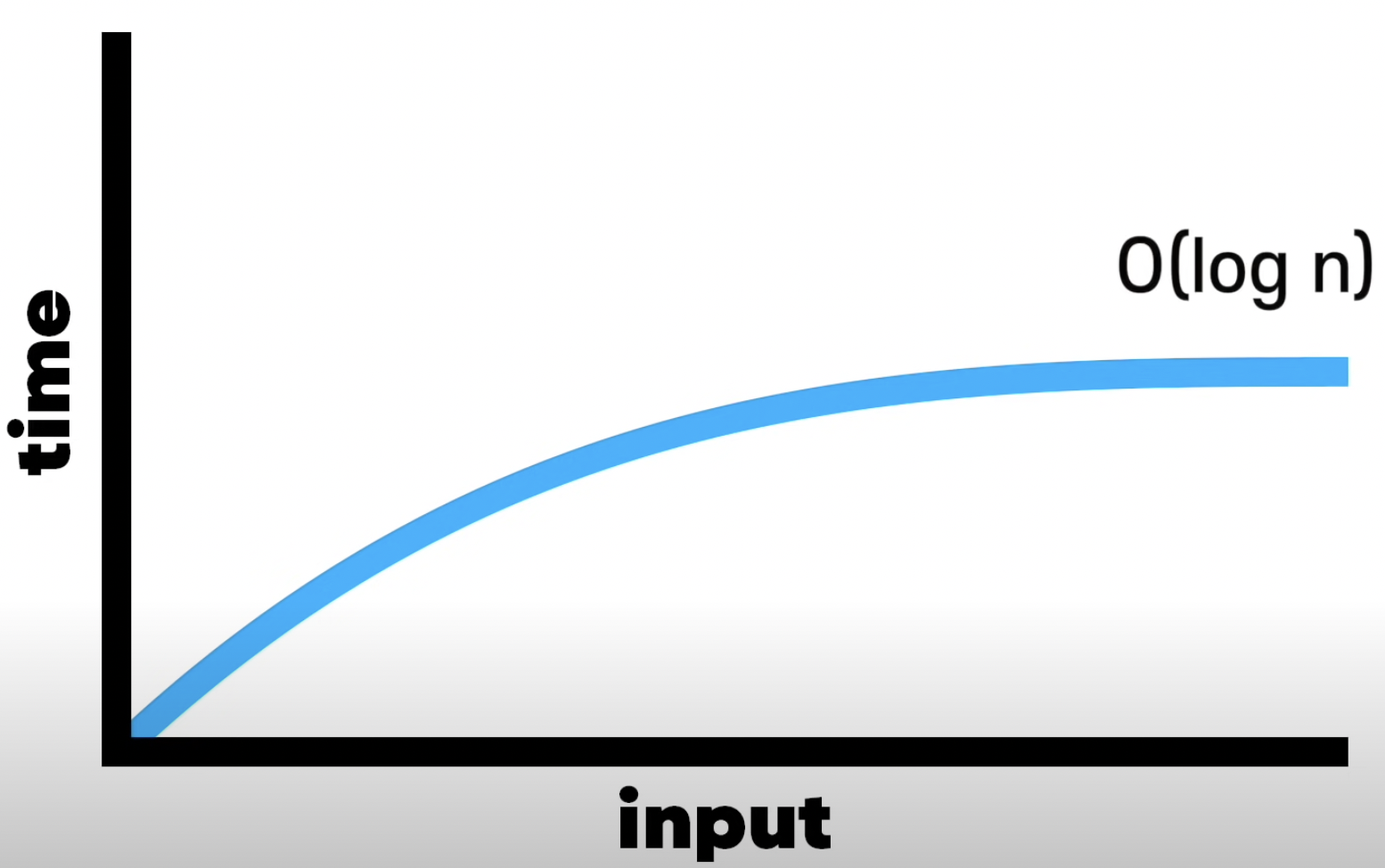
Untitled

로그 시간(Logarithmic Time)

로그(Log) 형태로 되어 있는 알고리즘으로 *이진검색(Binary Search) 알고리즘을 설명할 때 사용된다. O(Log N)으로 표기한다.

  • 로그(Log)처럼 계속 반으로 나누어 값을 찾아내는 알고리즘을 말한다.

Untitled